library(lubridate)
start_time_dt <- ymd_hms(start_time, tz = "Europe/Zurich")Ausgangssituation
Sie arbeiten als Data Analyst/in bei einem E-Scooter-Anbieter in der Schweiz. Ziel ist eine erste EDA von Daten zu Fahrten mit ihren E-Scootern, um (i) Nachfrage-Peaks über den Tag zu identifizieren, (ii) typische vs. auffällige Fahrten zu erkennen und (iii) zu prüfen, ob Abbrüche mit der Akkuwarnung zusammenhängen. Auf Basis Ihrer Ergebnisse sollen konkrete betriebliche Maßnahmen (z.B. Rebalancing-/Charging-Zeiten, Umgang mit Ausreissern, Priorisierung von Akku-Checks) abgeleitet werden.
Beschreibung der Daten
In der Woche vom 10.–17. Mai 2025 wurden Fahrten mit E-Scootern eines Anbieters als Testdatensatz in einer Schweizer Stadt (anonymisiert) protokolliert. Der Datensatz enthält 2’000 Fahrten.
Codebook: Variablenbeschreibung
Datensatz: scooter.csv Beobachtungseinheit: eine Zeile = eine Scooter-Fahrt (trip_id)
| Variable | Typ (wie geliefert) | Bedeutung | Einheit / Wertebereich |
|---|---|---|---|
trip_id |
Zahl | eindeutige Fahrten-ID | 1001… |
start_time |
Text | Startzeitpunkt der Fahrt | ISO-Zeitstempel als String |
scooter_type |
Text | Scooter-Modell | "Model A", "Model B" |
trip_distance_m |
Zahl | gefahrene Distanz | Meter |
trip_duration_s |
Zahl | Fahrtdauer | Sekunden |
user_rating |
Text | Rating durch Nutzer/in | "1"…"5" und "NA" |
battery_low |
logisch | Akkuwarnung bei Start | TRUE/FALSE |
trip_aborted |
logisch | Fahrt abgebrochen? | TRUE/FALSE |
Sie werden in dieser Aufgabe Datums- und Uhrzeitangaben im Rahmen des Data Wranglings anpassen müssen. Die state-of-the-art Library dazu ist lubridate die eine grosse Hilfe darstellt. Wenn es in der Aufgabe so weit ist, verwenden Sie die Informationen und Hinweise zu lubridate aus der nachfolgenden Box.
Warum lubridate?
Mit lubridate können Sie Zeitstempel (Strings) zuverlässig in Datum/Zeit umwandeln und bequem Bestandteile wie Tag, Wochentag oder Stunde extrahieren.
1) Zeitstempel parsen (String → Datum/Zeit)
Wenn start_time als Text vorliegt, müssen Sie ihn zuerst in ein datetime umwandeln:
Alternative Parser (je nach Format):
ymd()→ nur Datum (YYYY-MM-DD)mdy()→ US-Format (MM/DD/YYYY)dmy()→ (DD-MM-YYYY)ymd_hm()→ ohne Sekunden
2) Bestandteile extrahieren
hour(start_time_dt) # 0–23
minute(start_time_dt) # 0–59
second(start_time_dt) # 0–59
day(start_time_dt) # 1–31
month(start_time_dt) # 1–12 (oder month(..., label=TRUE))
year(start_time_dt)
wday(start_time_dt) # Wochentag als Zahl (1–7)Wochentag lesbar (z. B. “Sat”, “Sun”):
wday(start_time_dt, label = TRUE, abbr = TRUE)3) Datum/Zeit abrunden (für Aggregationen)
Das ist hilfreich, wenn Sie z. B. nach Stunde oder Tag zählen möchten:
floor_date(start_time_dt, unit = "hour") # auf volle Stunde
floor_date(start_time_dt, unit = "day") # auf Mitternacht (Tagesstart)4) Zeitdifferenzen & Dauer
Wenn Sie Zeiten vergleichen oder Differenzen bilden möchten:
difftime(t2, t1, units = "mins")Oder eine Dauer direkt aus Sekunden:
as.duration(trip_duration_s)5) Nützliche Tipps (typisch in mutate())
mutate(
start_time = ymd_hms(start_time, tz = "Europe/Zurich"),
start_hour = hour(start_time),
weekday = wday(start_time, label = TRUE, abbr = TRUE)
)Noch mehr Informationen über Lubridate?
Aufgabe 1: Import & erste Orientierung
Laden Sie die Rohdatendatein scooter_mini.csv aus Moodle herunter.
1.1 Import des Datensatzes
Laden Sie scooter.csv in RStudio. Wie viele verschiedene Scooter-Modelle (scooter_type) wurden verwendet?
Code anzeigen
library(tidyverse)
scooter <- read_csv("data/scooter.csv", show_col_types = FALSE)
counts <- scooter %>% count(scooter_type)
counts# A tibble: 2 × 2
scooter_type n
<chr> <int>
1 Model A 1058
2 Model B 942Code anzeigen
n_A <- counts %>% filter(scooter_type == "Model A") %>% pull(n)
n_B <- counts %>% filter(scooter_type == "Model B") %>% pull(n)Es wurden zwei E-Scootermodelel verwendet, A und B: Model A (1058) und Model B (942).
1.2 Variablentypen und Auffälligkeiten in den Daten
Welche Variablen sind numerisch, welche kategorial? Nennen Sie mindestens 2 Variablen pro Typ und begründen Sie kurz. Gibt es Auffälligkeiten?
Code anzeigen
glimpse(scooter)Rows: 2,000
Columns: 8
$ trip_id <dbl> 1001, 1002, 1003, 1004, 1005, 1006, 1007, 1008, 1009, …
$ start_time <dttm> 2025-05-10 02:30:08, 2025-05-10 02:50:03, 2025-05-10 …
$ scooter_type <chr> "Model B", "Model A", "Model B", "Model A", "Model A",…
$ battery_low <lgl> FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, TRUE,…
$ user_rating <dbl> 5, 3, 5, 3, 5, 4, NA, NA, 3, 4, 5, 3, 3, 4, 4, 2, 5, 2…
$ trip_distance_m <dbl> 1457, NA, 804, 364, 1196, 922, 1721, NA, 2765, NA, 190…
$ trip_duration_s <dbl> 442.6771, NA, 142.8495, 98.1066, 221.0982, 154.9919, 3…
$ trip_aborted <lgl> TRUE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE,…Code anzeigen
summary(scooter) trip_id start_time scooter_type
Min. :1001 Min. :2025-05-10 02:30:08 Length:2000
1st Qu.:1501 1st Qu.:2025-05-11 11:30:50 Class :character
Median :2000 Median :2025-05-12 21:50:29 Mode :character
Mean :2000 Mean :2025-05-13 05:58:24
3rd Qu.:2500 3rd Qu.:2025-05-14 22:45:55
Max. :3000 Max. :2025-05-17 01:45:12
battery_low user_rating trip_distance_m trip_duration_s
Mode :logical Min. :1.000 Min. : 217.0 Min. : 26.18
FALSE:1617 1st Qu.:3.000 1st Qu.: 839.8 1st Qu.: 207.74
TRUE :383 Median :4.000 Median : 1242.0 Median : 323.20
Mean :3.462 Mean : 1590.2 Mean : 418.98
3rd Qu.:4.000 3rd Qu.: 1875.0 3rd Qu.: 495.46
Max. :5.000 Max. :12000.0 Max. :4740.29
NA's :150 NA's :60 NA's :60
trip_aborted
Mode :logical
FALSE:1724
TRUE :276
1) Missing Values sind enthalten: * trip_distance_m: 60 NA * trip_duration_s: 60 NA * user_rating: 150 NA
2) Datentypen: * user_rating, trip_duration, trip_distance_msind numerisch * start_timeist ein Datumsformat * scooter_type müsste kategorial sein, ist hier aber als string deklariert. * trip_aborted und battery_low sind logisch (true/false)
Aufgabe 2: Data Wrangling
2.1 Erstellen Sie eine neue Spalte duration_min, die die Fahrtdauer in Minuten. Stören die NAs die Umrechnung (Datentransformation). Begründen Sie kurz?
Code anzeigen
library(lubridate)
scooter <- scooter %>%
mutate(trip_duration_min = trip_duration_s/60)
summary(scooter) trip_id start_time scooter_type
Min. :1001 Min. :2025-05-10 02:30:08 Length:2000
1st Qu.:1501 1st Qu.:2025-05-11 11:30:50 Class :character
Median :2000 Median :2025-05-12 21:50:29 Mode :character
Mean :2000 Mean :2025-05-13 05:58:24
3rd Qu.:2500 3rd Qu.:2025-05-14 22:45:55
Max. :3000 Max. :2025-05-17 01:45:12
battery_low user_rating trip_distance_m trip_duration_s
Mode :logical Min. :1.000 Min. : 217.0 Min. : 26.18
FALSE:1617 1st Qu.:3.000 1st Qu.: 839.8 1st Qu.: 207.74
TRUE :383 Median :4.000 Median : 1242.0 Median : 323.20
Mean :3.462 Mean : 1590.2 Mean : 418.98
3rd Qu.:4.000 3rd Qu.: 1875.0 3rd Qu.: 495.46
Max. :5.000 Max. :12000.0 Max. :4740.29
NA's :150 NA's :60 NA's :60
trip_aborted trip_duration_min
Mode :logical Min. : 0.4364
FALSE:1724 1st Qu.: 3.4623
TRUE :276 Median : 5.3866
Mean : 6.9830
3rd Qu.: 8.2577
Max. :79.0049
NA's :60 Die NA-Werte stören bei der Umrechnung selbst nicht: Wenn trip_duration_s fehlt, wird duration_min automatisch ebenfalls NA (Missingness “propagiert”). Sie werden erst problematisch: * Funktionen wie mean() liefern ohne Zusatz standardmäßig NA, sobald Missing Values enthalten sind.
→ Verwenden Sie dann z. B. mean(duration_min, na.rm = TRUE). * Bei vielen ggplot2-Geoms werden NA-Beobachtungen automatisch weggelassen (ggf. mit Hinweis).
→ Vorsicht, hier werden Informationen vernachlässigt.
2.2 Entfernung Fahrten < 1 Min.
Häufig kommt es zu Fehlern z.B. bei der Initialisierung des Fahrzeugs und der Vorgang wird abgebrochen. Wir wollen alle Fahrten mit trip_duration_min < 1 Min. entfernen. Warum ist die naheliegende Codelösung: scooter %>% filter(trip_duration_min >= 1) problematisch? Analysieren Sie das summary(scooter) , was fällt auf? Wie kann man es korrekt machen?
Code anzeigen
scooter %>%
filter(trip_duration_min >= 1) %>%
summary() trip_id start_time scooter_type
Min. :1001 Min. :2025-05-10 02:30:08 Length:1920
1st Qu.:1496 1st Qu.:2025-05-11 11:19:18 Class :character
Median :1992 Median :2025-05-12 21:20:12 Mode :character
Mean :1997 Mean :2025-05-13 05:37:37
3rd Qu.:2493 3rd Qu.:2025-05-14 22:01:44
Max. :3000 Max. :2025-05-17 01:45:12
battery_low user_rating trip_distance_m trip_duration_s
Mode :logical Min. :1.000 Min. : 254.0 Min. : 61.36
FALSE:1547 1st Qu.:3.000 1st Qu.: 849.5 1st Qu.: 210.62
TRUE :373 Median :4.000 Median : 1251.0 Median : 324.98
Mean :3.469 Mean : 1602.8 Mean : 422.83
3rd Qu.:4.000 3rd Qu.: 1879.0 3rd Qu.: 497.23
Max. :5.000 Max. :12000.0 Max. :4740.29
NA's :137
trip_aborted trip_duration_min
Mode :logical Min. : 1.023
FALSE:1650 1st Qu.: 3.510
TRUE :270 Median : 5.416
Mean : 7.047
3rd Qu.: 8.287
Max. :79.005
Würde man so filtern, werden nicht nur die Werte >=1 eliminiert, sondern auch alle Fahrten die in trip_duration_min ein NA besitzen. Vielleicht sind aber die Informationen über die anderen Variablen wichtig und interessant, deshalb sollte man vorerst versuchen die NAs zu behalten. Wie kann man es besser machen?
Code anzeigen
scooter %>%
mutate(trip_duration_min = trip_duration_s / 60) %>%
filter(is.na(trip_duration_min) | trip_duration_min >= 1) %>%
summary() trip_id start_time scooter_type
Min. :1001 Min. :2025-05-10 02:30:08 Length:1980
1st Qu.:1498 1st Qu.:2025-05-11 11:24:07 Class :character
Median :1998 Median :2025-05-12 21:35:16 Mode :character
Mean :1999 Mean :2025-05-13 05:50:03
3rd Qu.:2497 3rd Qu.:2025-05-14 22:23:03
Max. :3000 Max. :2025-05-17 01:45:12
battery_low user_rating trip_distance_m trip_duration_s
Mode :logical Min. :1.00 Min. : 254.0 Min. : 61.36
FALSE:1600 1st Qu.:3.00 1st Qu.: 849.5 1st Qu.: 210.62
TRUE :380 Median :4.00 Median : 1251.0 Median : 324.98
Mean :3.47 Mean : 1602.8 Mean : 422.83
3rd Qu.:4.00 3rd Qu.: 1879.0 3rd Qu.: 497.23
Max. :5.00 Max. :12000.0 Max. :4740.29
NA's :149 NA's :60 NA's :60
trip_aborted trip_duration_min
Mode :logical Min. : 1.023
FALSE:1706 1st Qu.: 3.510
TRUE :274 Median : 5.416
Mean : 7.047
3rd Qu.: 8.287
Max. :79.005
NA's :60 Bei trip_abortedsehen wir, dass einige Fahrten eliminiert wurden. Jetzt filtern wir scooter richtig:
Code anzeigen
scooter <- scooter %>%
mutate(trip_duration_min = trip_duration_s / 60) %>%
filter(is.na(trip_duration_min) | trip_duration_min >= 1)
summary(scooter) trip_id start_time scooter_type
Min. :1001 Min. :2025-05-10 02:30:08 Length:1980
1st Qu.:1498 1st Qu.:2025-05-11 11:24:07 Class :character
Median :1998 Median :2025-05-12 21:35:16 Mode :character
Mean :1999 Mean :2025-05-13 05:50:03
3rd Qu.:2497 3rd Qu.:2025-05-14 22:23:03
Max. :3000 Max. :2025-05-17 01:45:12
battery_low user_rating trip_distance_m trip_duration_s
Mode :logical Min. :1.00 Min. : 254.0 Min. : 61.36
FALSE:1600 1st Qu.:3.00 1st Qu.: 849.5 1st Qu.: 210.62
TRUE :380 Median :4.00 Median : 1251.0 Median : 324.98
Mean :3.47 Mean : 1602.8 Mean : 422.83
3rd Qu.:4.00 3rd Qu.: 1879.0 3rd Qu.: 497.23
Max. :5.00 Max. :12000.0 Max. :4740.29
NA's :149 NA's :60 NA's :60
trip_aborted trip_duration_min
Mode :logical Min. : 1.023
FALSE:1706 1st Qu.: 3.510
TRUE :274 Median : 5.416
Mean : 7.047
3rd Qu.: 8.287
Max. :79.005
NA's :60 2.3 Fehlende Werte
In der Variablen trip_distance_m gibt es Werte, die fehlen. Wie hoch ist ihr Anteil an allen Beobachtungen und wenn sie unter 10% sind entfernen Sie sie.
Code anzeigen
# Anzahl und Anteil fehlender Distanzwerte
summary(scooter$trip_distance_m) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
254.0 849.5 1251.0 1602.8 1879.0 12000.0 60 Code anzeigen
na_dist <- sum(is.na(scooter$trip_distance_m))
n_total <- nrow(scooter)
na_dist[1] 60Code anzeigen
na_dist / n_total[1] 0.03030303Da der Anteil bei ca. 3% der Beobachtungen (hier Fahrten) liegt, können wir diese löschen ohne zu befürchten, dass wir wichtige Informationen verlieren.
Code anzeigen
scooter <- scooter %>%
filter(!is.na(trip_distance_m))
summary(scooter$trip_distance_m) Min. 1st Qu. Median Mean 3rd Qu. Max.
254.0 849.5 1251.0 1602.8 1879.0 12000.0 Code anzeigen
nrow(scooter)[1] 1920Hier sehen wir jetzt, dass durch die beiden Filterschritte 68 Fahrten entfernt wurden.
2.4 Erzeugung neuer Variablen
Unser Management interessiert sich vor allem dafür, zu welchen Uhrzeiten und an welchen Wochentagen die Nutzer ihren E-Scooter verwenden. Generieren Sie die beiden neuen Variablen start_hour und weekday erzeugen.
Code anzeigen
scooter <- scooter %>%
mutate(
start_hour = hour(start_time),
weekday = wday(start_time, label = TRUE, abbr = TRUE)
)
summary(scooter) trip_id start_time scooter_type
Min. :1001 Min. :2025-05-10 02:30:08 Length:1920
1st Qu.:1496 1st Qu.:2025-05-11 11:19:18 Class :character
Median :1992 Median :2025-05-12 21:20:12 Mode :character
Mean :1997 Mean :2025-05-13 05:37:37
3rd Qu.:2493 3rd Qu.:2025-05-14 22:01:44
Max. :3000 Max. :2025-05-17 01:45:12
battery_low user_rating trip_distance_m trip_duration_s
Mode :logical Min. :1.000 Min. : 254.0 Min. : 61.36
FALSE:1547 1st Qu.:3.000 1st Qu.: 849.5 1st Qu.: 210.62
TRUE :373 Median :4.000 Median : 1251.0 Median : 324.98
Mean :3.469 Mean : 1602.8 Mean : 422.83
3rd Qu.:4.000 3rd Qu.: 1879.0 3rd Qu.: 497.23
Max. :5.000 Max. :12000.0 Max. :4740.29
NA's :137
trip_aborted trip_duration_min start_hour weekday
Mode :logical Min. : 1.023 Min. : 0.00 Sun:345
FALSE:1650 1st Qu.: 3.510 1st Qu.:10.00 Mon:250
TRUE :270 Median : 5.416 Median :14.00 Tue:246
Mean : 7.047 Mean :13.93 Wed:223
3rd Qu.: 8.287 3rd Qu.:18.00 Thu:228
Max. :79.005 Max. :23.00 Fri:230
Sat:398 Aufgabe 3: Datenvisualisierung, Kennwerte (Metriken)
3.1 Wie verteilt sich die durchschnittliche Fahrtdauer auf die Wochentage?
Code anzeigen
scooter %>%
group_by(weekday) %>%
summarise(
mean_duration = mean(trip_duration_min, na.rm = TRUE),
n = n()
) %>%
arrange(weekday)# A tibble: 7 × 3
weekday mean_duration n
<ord> <dbl> <int>
1 Sun 7.03 345
2 Mon 7.39 250
3 Tue 7.23 246
4 Wed 7.56 223
5 Thu 7.04 228
6 Fri 6.48 230
7 Sat 6.78 398Es sieht so aus, dass die Anzahl Fahrten kaum vom Wochentag abhängt.
Formulierungsvorschlag (für die Aufgabenstellung, 3–4 Sätze)
Sie arbeiten als Data Analyst*in bei einem E-Scooter-Anbieter. Ziel ist eine erste EDA, um (i) Nachfrage-Peaks über den Tag zu identifizieren, (ii) typische vs. auffällige Fahrten zu erkennen und (iii) zu prüfen, ob Abbrüche mit der Akkuwarnung zusammenhängen. Auf Basis Ihrer Ergebnisse sollen konkrete betriebliche Maßnahmen (z.B. Rebalancing-/Charging-Zeiten, Umgang mit Ausreißern, Priorisierung von Akku-Checks) abgeleitet werden.
Code anzeigen
scooter %>%
count(start_hour) %>%
ggplot(aes(x = start_hour, y = n)) +
geom_col() +
labs(x = "Startstunde (0–23)", y = "Anzahl Fahrten")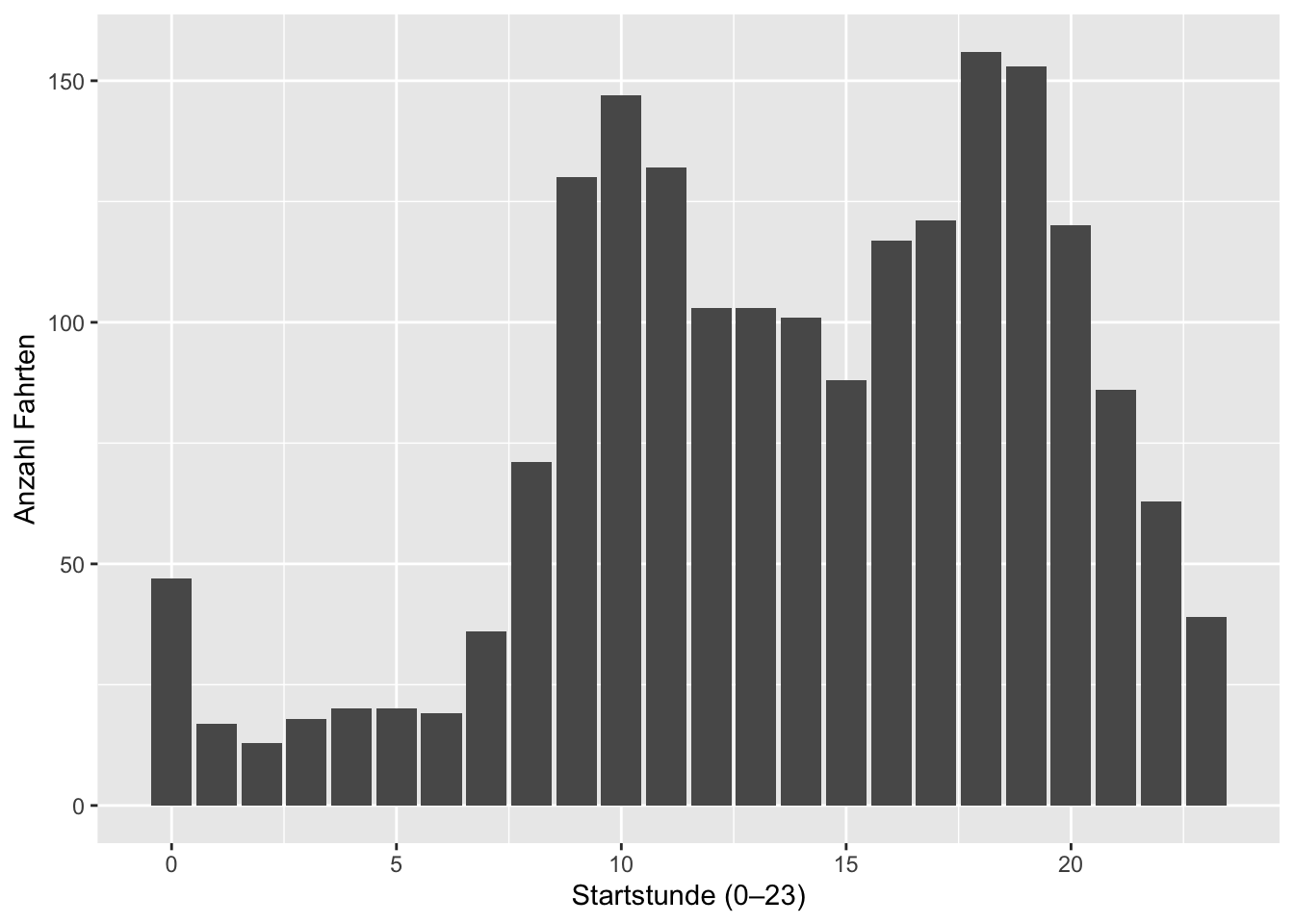
Beschreibung des Histogramms
Das Histogramm zeigt die Anzahl Fahrten pro Startstunde (0–23). Die Verteilung ist nicht gleichmäßig: In der Nacht gibt es deutlich weniger Fahrten, während es tagsüber zwei klare Nachfragephasen gibt. Besonders auffällig sind erhöhte Fahrtenzahlen am Vormittag (typisch „Start in den Tag“) und ein weiterer Peak am späten Nachmittag/Abend (typisch „Feierabend/Freizeit“). Insgesamt deutet die Verteilung auf ein tageszeitabhängiges Nutzungsverhalten hin.
Diskussion: Warum ist das fürs Business relevant?
Für den Anbieter ist dieses Muster operativ wichtig, weil die Verfügbarkeit der Scooter genau dann stimmen muss, wenn die Nachfrage hoch ist. Aus dem Histogramm lassen sich daher konkrete Maßnahmen ableiten:
- Service-/Charging-Zeiten planen: In Zeiten mit niedriger Nachfrage (Nacht/Frühmorgen) lassen sich Scooter effizient einsammeln, laden und wieder ausbringen, ohne viele potenzielle Fahrten zu verlieren.
- Verfügbarkeit in Peak-Zeiten sichern: Vor den Peaks sollten genug einsatzbereite Scooter bereitstehen (z.B. an Hotspots). Sonst entstehen „verpasste Fahrten“ → weniger Umsatz.
- Kapazitäten priorisieren: Personal, Logistik und Ladeinfrastruktur können auf die Stunden mit dem höchsten Einfluss konzentriert werden (statt gleichmäßig über den Tag).
- Hypothesen für nächste Analysen: Peaks werfen Folgefragen auf: Sind Fahrten in Peak-Zeiten kürzer (Pendeln) oder länger (Freizeit)? Genau dafür lohnt sich als nächster Schritt ein Boxplot der Fahrtdauer nach Tageszeit.
3.2 Welche Fahrtdauern und -distanzen sind „typisch“ und welche sind Ausreißer?
Erstellen Sie Boxplots der Fahrtdauer (trip_duration_min)/ Dauer (trip_distance_m) nach Tageszeit-Klasse und bestimmen Sie die Kennwerte (IQR, Mean, Median).
Diskutieren Sie kurz: Was bedeutet das für die Akkulaufzeit und die erwartete Anzahl Fahrten pro Scooter (bei gleicher Verfügbarkeit)?
Code anzeigen
library(lubridate)
scooter <- scooter %>%
mutate(
start_hour = hour(start_time),
time_block = case_when(
start_hour %in% 0:5 ~ "Nacht (0–5)",
start_hour %in% 6:9 ~ "Morgen (6–9)",
start_hour %in% 10:15 ~ "Tag (10–15)",
start_hour %in% 16:19 ~ "Abend (16–19)",
TRUE ~ "Spät (20–23)"
),
time_block = factor(time_block,
levels = c("Nacht (0–5)","Morgen (6–9)","Tag (10–15)","Abend (16–19)","Spät (20–23)"))
)
ggplot(scooter, aes(x = time_block, y = trip_duration_min)) +
geom_boxplot() +
labs(x = "Tageszeit-Klasse", y = "Fahrtdauer (Minuten)")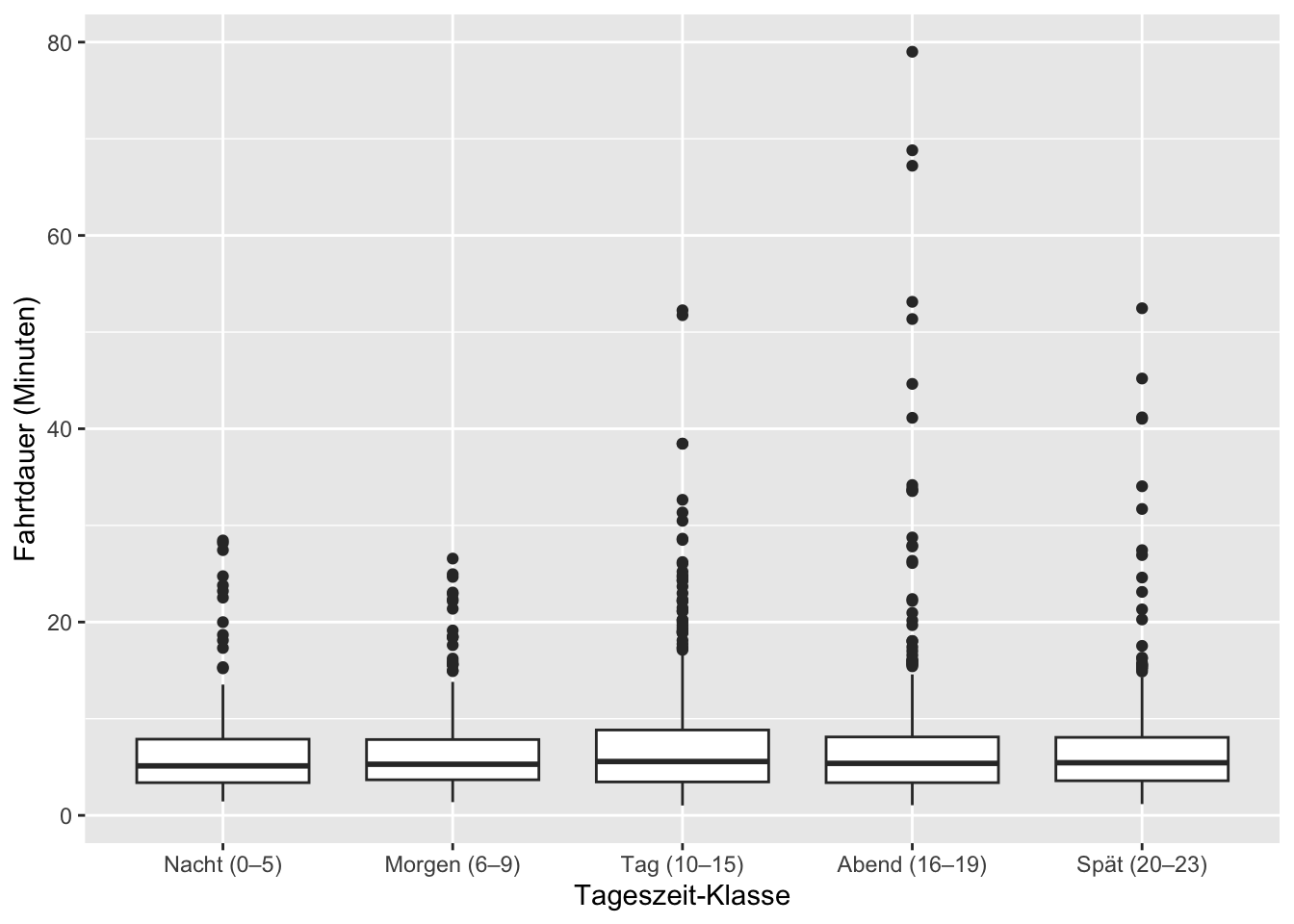
Für die Kennwerte der Zeit:
Code anzeigen
scooter %>%
group_by(time_block) %>%
summarise(
n = n(),
mean_duration = mean(trip_duration_min, na.rm = TRUE),
median_duration = median(trip_duration_min, na.rm = TRUE),
iqr_duration = IQR(trip_duration_min, na.rm = TRUE)
) %>%
arrange(time_block)# A tibble: 5 × 5
time_block n mean_duration median_duration iqr_duration
<fct> <int> <dbl> <dbl> <dbl>
1 Nacht (0–5) 135 6.87 5.12 4.50
2 Morgen (6–9) 256 6.66 5.29 4.16
3 Tag (10–15) 674 7.19 5.57 5.37
4 Abend (16–19) 547 7.08 5.38 4.73
5 Spät (20–23) 308 7.08 5.44 4.49Zum Vergleich die Boxplots der Kennwerte der Distanz:
Code anzeigen
scooter <- scooter %>%
mutate(
start_hour = hour(start_time),
time_block = case_when(
start_hour %in% 0:5 ~ "Nacht (0–5)",
start_hour %in% 6:9 ~ "Morgen (6–9)",
start_hour %in% 10:15 ~ "Tag (10–15)",
start_hour %in% 16:19 ~ "Abend (16–19)",
TRUE ~ "Spät (20–23)"
),
time_block = factor(time_block,
levels = c("Nacht (0–5)","Morgen (6–9)","Tag (10–15)","Abend (16–19)","Spät (20–23)"))
)
ggplot(scooter, aes(x = time_block, y = trip_distance_m)) +
geom_boxplot() +
labs(x = "Tageszeit-Klasse", y = "Distanz (Meilen)")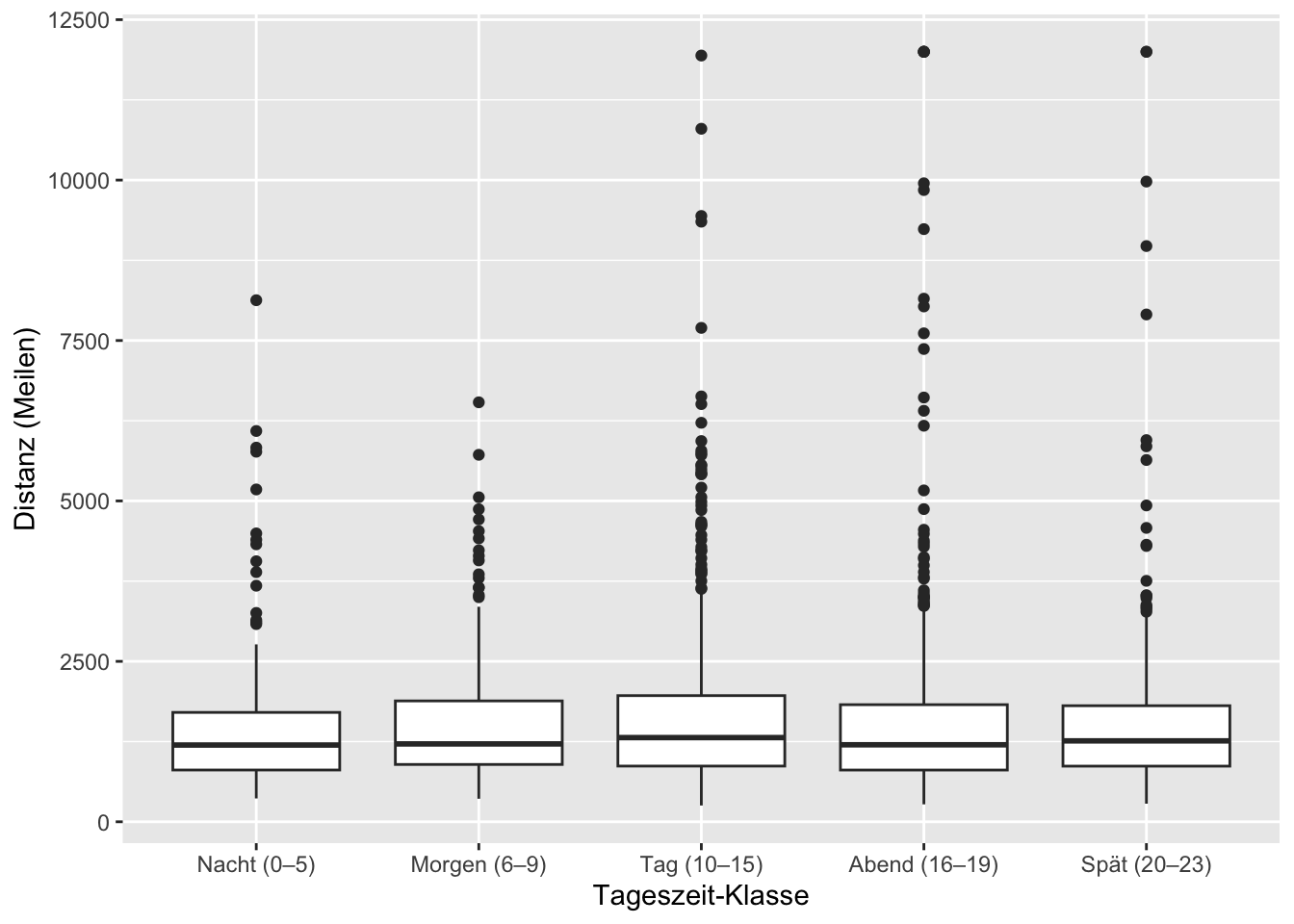
Noch die Kennwerte zur Distanz:
Code anzeigen
scooter %>%
group_by(scooter_type) %>%
summarise(
n = n(),
mean_distance = mean(trip_distance_m, na.rm = TRUE),
median_distance = median(trip_distance_m, na.rm = TRUE),
q1_distance = quantile(trip_distance_m, probs = 0.25, na.rm = TRUE),
q3_distance = quantile(trip_distance_m, probs = 0.75, na.rm = TRUE),
iqr_distance = IQR(trip_distance_m, na.rm = TRUE)
)# A tibble: 2 × 7
scooter_type n mean_distance median_distance q1_distance q3_distance
<chr> <int> <dbl> <dbl> <dbl> <dbl>
1 Model A 1014 1623. 1242 844. 1872.
2 Model B 906 1580. 1258 858 1896.
# ℹ 1 more variable: iqr_distance <dbl>Diskussion:
- Bei den Boxplots zu den Tageszeitklassen, sehen wir, dass die Fahrten laut Median im Mittel nur etwas mehr als 5 Min. dauern. Wir sehen auch, dass die Verteilung rechtsschief sein muss, da der Mean in allen Tagesklassen höher liegt als der Median. Hier ist der Median aussagekräftiger als der Mean! - In allen Klassen treten Ausreisser auf, wobei die grössten zwischen 10-0 Uhr auftreten, d.h. deutlich längere Fahrten gemacht werden oder die E-Scooter ohne Abmeldung längere Zeit parken. - Bei den Distanzen ein ähnliches Verhalten, wie bei den Zeiten. Hier liegt der Median bei ca. 1600 m und das Streuverhalten ist bei beiden E-Scooter Modellen gleich. Typischerweise werden Distanzen zwischen ca. 850 (Q1) und 1870 m (Q3) zurückgelegt.
Relevanz für das Unternehmen: Welche Schlüsse ziehen wir daraus für das Business?
a) Fahrtdauer nach Tageszeit (Boxplots + Kennwerte)
Kapazitätsplanung / Umsatz pro Scooter Wenn die typische Fahrt nur ~5 Minuten dauert, kann ein verfügbarer Scooter viele Fahrten pro Tag ermöglichen – sofern er geladen ist und am richtigen Ort steht. → KPI-Idee: Fahrten pro Scooter-Tag hängt stark an typischer Fahrtdauer und Verfügbarkeit.
Akku- und Serviceplanung Längere Fahrten in bestimmten Zeitfenstern bedeuten schnellere Entladung und potenziell mehr “battery_low”-Situationen. → Charging-/Service-Routen bevorzugt vor Peak-Zeiten planen (nicht mitten im Peak).
Ausreißer sind operativ relevant Sehr lange Fahrten können zwei Ursachen haben:
- echte lange Fahrten (höherer Akkuverschleiß, ggf. andere Preislogik),
- oder Fehlbuchungen / nicht korrekt beendete Fahrten (App-Prozess, Geofencing, Backend). → Maßnahme: Diese Fälle taggen (z.B.
trip_duration_min > Q3 + 1.5*IQR) und separat prüfen, weil sie Kennzahlen verzerren und potenziell Kosten verursachen.
b) Distanz nach Scooter-Modell (Boxplot)
Modelle werden ähnlich genutzt → gleiche Einsatzstrategie plausibel Wenn die Distanzverteilungen sehr ähnlich sind, gibt es keinen starken Hinweis, dass ein Modell ein anderes Nutzersegment bedient. → Gleiche Rebalancing-/Charging-Logik für beide Modelle ist vertretbar.
Typische Distanz = Grundlage für Akku-Reichweitenrechnung Mit einer typischen Distanz um ~1–2 km lässt sich (zusammen mit Akku-Kapazität/Verbrauch) abschätzen:
- Fahrten pro Ladung (zentral für Profitabilität),
- erwartete Ladefrequenz pro Scooter.
Ausreißer nachts sind ein Signal Lange Nachtfahrten können real sein (z.B. Heimweg), aber auch Missbrauch/Fehlmessung. → Operativ interessant: Nacht-Ausreißer separat monitoren (Risikoprofil, Supportfälle, Vandalismus/Diebstahlindikatoren).
3.3 Abbruchquote wegen battery_low
Einer Kollegin ist noch etwas aufgefallen. Wieviele Fahrten “verlieren” wir, weil der Batteriestand zu niedrig ist, d.h. ein Kunde oder Kundin befürchtet aufgrund des Batteriestandes nicht bis ans Ziel zu gelangen?
Analysieren Sie hierfür, ob die Abbruchrate bei niedrigem Batteriestand höher ist und visualisieren Sie den Zusammenhang mit einem Balkendiagramm.
Code anzeigen
scooter %>%
group_by(battery_low) %>%
summarise(
n = n(),
abort_rate = mean(trip_aborted, na.rm = TRUE)
)# A tibble: 2 × 3
battery_low n abort_rate
<lgl> <int> <dbl>
1 FALSE 1547 0.116
2 TRUE 373 0.241Code anzeigen
scooter %>%
group_by(battery_low) %>%
summarise(abort_rate = mean(trip_aborted, na.rm = TRUE)) %>%
ggplot(aes(x = battery_low, y = abort_rate)) +
geom_col() +
labs(x = "Akkustand-Warnung (battery_low)", y = "Abbruchrate")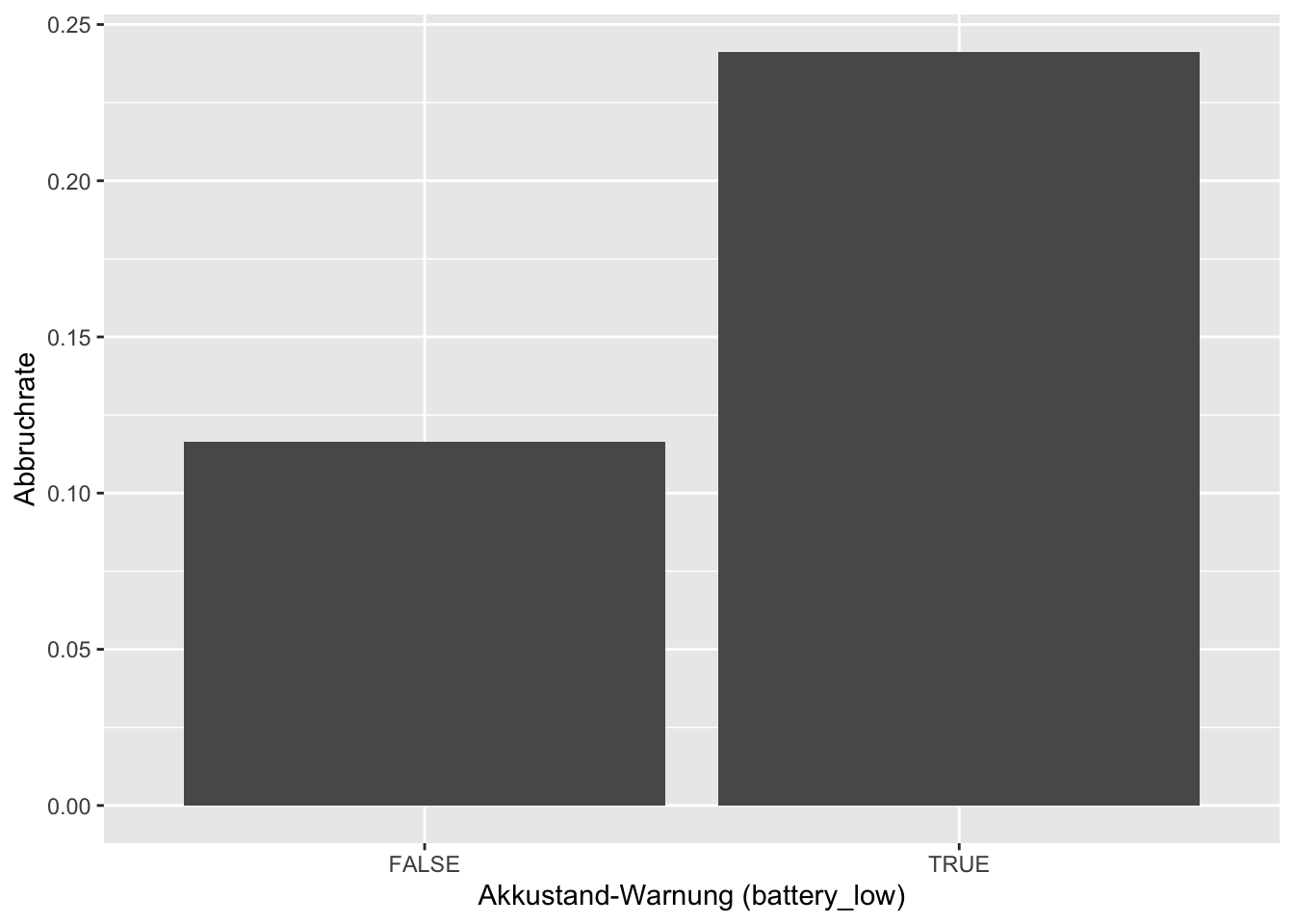
Wir erkennen, dass im Fall, dass battery_lowangezeigt wird die Abbruchrate ungefährt doppelt so hoch ist, wie sonst. Schaut man auf die absulten Fallzahlen, so verlieren wir von 2000 möglichen Fahrten 373 aufgrund unzureichenden Batteriestandes. Um noch etwas für den Serviceplan zu lernen plotten wir noch die verlorenen Fahrten in Abhängigkeit der Tageszeitklasse.
3.4 Verlorene Fahrten
Ihr Businessanalyst sagt, die Abbruchraten sagen zwar etwas über das Risiko aus, dass ein Kunde oder eine Kundin die Fahrt erst gar nicht antritt, aber wo verlieren wir das meiste Geld während des Tages? Plotten Sie um dies zu beantworten ein Balkendiagramm der Anzahl “verlorener” Fahrten pro Tageszeitklasse.
Code anzeigen
scooter %>%
group_by(time_block) %>%
summarise(lost_trips = sum(trip_aborted, na.rm = TRUE)) %>%
ggplot(aes(x = time_block, y = lost_trips)) +
geom_col() +
labs(x = "Tageszeit-Klasse", y = "Verlorene Fahrten (Abbrüche)")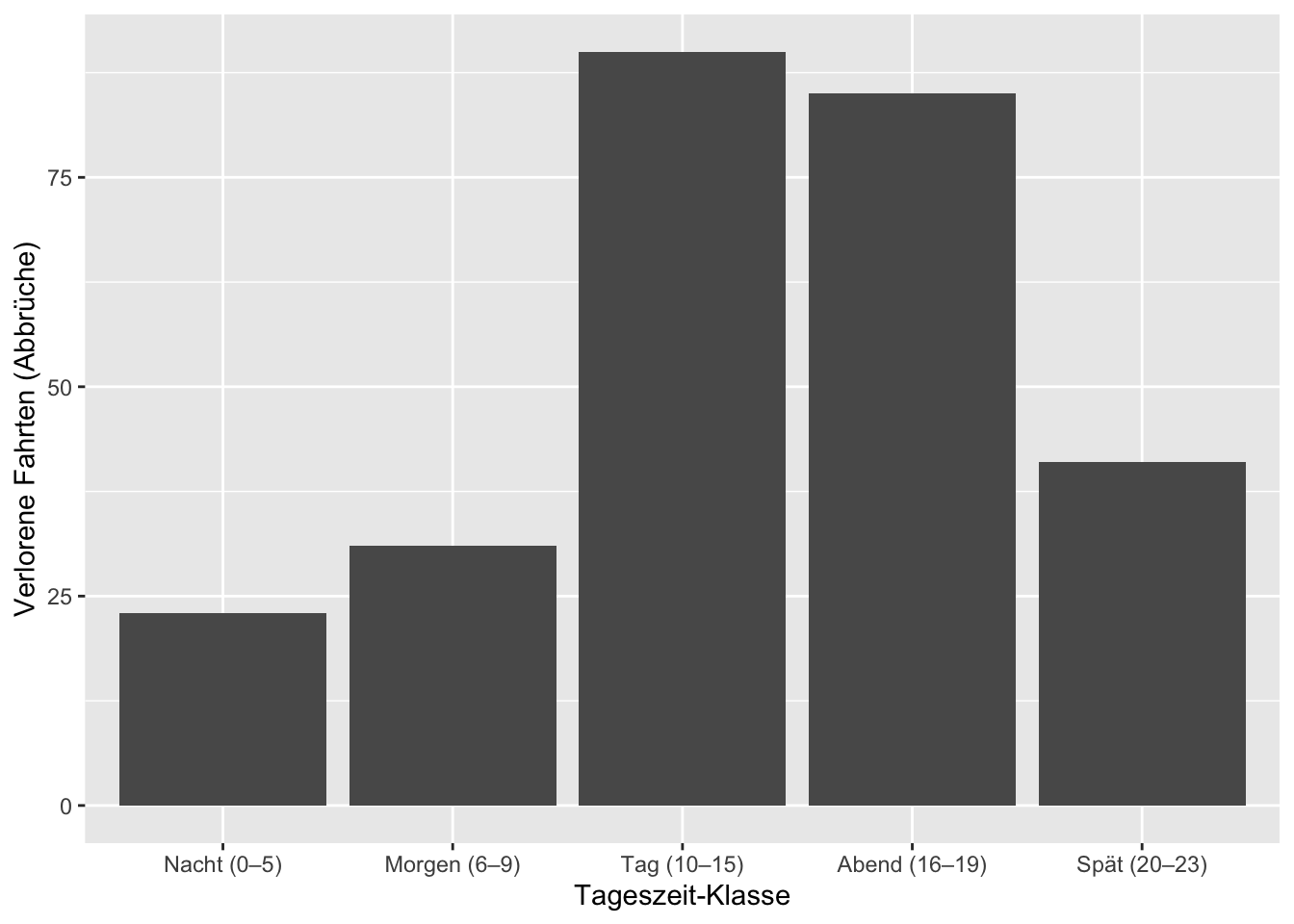
Wir sehen aus dem Balkendiagramm, dass wir zwischen 10-20 Uhr die meisten Abbrüche und damit auch die höchsten Einnahmeverluste erwarten. Für diese Tageszeiten müssen mehr geladene E-Scooter bereitgestellt
Aufgabe 4: Nächste mögliche Schritte
Sie haben schon einige Einblicke in die Eigenschaften der Daten erhalten. Im zyklischen Ablauf der EDA wäre nun eine neue Frage/Hypothese an die Daten zu formulieren. Welchen interessanten Fragen könnte man als nächstes nachgehen? Hier ein paar mögliche Überlegungen:
Bisher haben wir die fehlenden Werte noch nicht analysiert. Hierzu müss man jede E-Scotter mit fehlenden Werten. Hier wäre es interessant zu untersuchen, ob sie in allen Tageszeitklassen und Wochentagen gleichmässig auftreten. Wenn z.B. nur Nachts, gibt es ein GPS/Connectivity Problem mit den E-Scootern? Oder Problem mit der App, die auffällig sind?
Auch die Abbrüche haben wir nur grob untersucht mit ja/nein, aber nicht im Zusammenhang mit der Tageszeit oder der Warnung battery low. Vielleicht treten sie auch oft bei langen Fahrten auf, weil Kunden die Reichweite unterschätzt haben? Daraus könnte man lernen, ob es sich lohnen würde Fahrzeuge präventiv (also vor dem battery low Signal) einzusammeln bei hoher Nachfrage nach langen Fahrten.
Die Ausreisser wurden bisher nur am Rande im Zusammenhang mit den Boxplots diskutiert. Haben wir es bei Ausreissern bei der Dauer und Distanz immer mit “echten” langen Fahrten zu tun, oder tritt z.B. eine lange Dauer, aber sehr kurze Distanz auf? Parken die Kunden das Fahrzeug ohne sich auszuloggen? Oder gibt es Fehlermeldungen und Ausfälle des GPS Signals? Ähnlich bei grossen Distanzen, aber kurzer Dauer? Passen die berechneten Geschwindigkeiten zur 20 km/h Limitierung der Fahrzeuge? Wenn nicht, wurde die Dauer korrekt erfasst? Oder wurde bergab gefahren und die Geschwindigkeit hat eine natürliche Erklärung?
Noch viele solcher Fragen können formuliert werden. In der Praxis entscheidet, wofür wir uns interessieren.
Zusammenfassung der EDA
Zentrale Einsichten aus der EDA
- Nachfrage ist tageszeitabhängig: Es gibt klare Häufungen (z. B. morgens und am späten Nachmittag/Abend) und deutlich weniger Fahrten in der Nacht.
- Typische Fahrten sind kurz: Der Median der Fahrtdauer liegt bei wenigen Minuten; die Verteilung ist rechtsschief (Mittelwert > Median), d. h. wenige lange Fahrten ziehen den Durchschnitt nach oben.
- Ausreißer sind operativ relevant: Sehr lange Fahrten können echte Sonderfälle sein, aber auch auf Prozess-/Datenprobleme hindeuten (z. B. Fahrt nicht korrekt beendet).
- Modelle werden ähnlich genutzt: Die Distanzverteilungen von Model A und B sind vergleichbar (ähnlicher Median/IQR) → keine starke Segmentierung nach Modell erkennbar.
- Abbrüche müssen nach Impact priorisiert werden: Für die Planung ist nicht nur die Abbruchrate, sondern vor allem die Anzahl Abbrüche in Peak-Zeiten entscheidend (hohe Nachfrage ⇒ hoher potenzieller Umsatzverlust).
Abgeleitete Maßnahmen für den Betrieb
- Service-/Charging-Fenster in Nachfrage-Tälern legen (z. B. nachts), um die Verfügbarkeit in Peak-Zeiten zu maximieren.
- Rebalancing/Umverteilung vor Peaks priorisieren, damit genug Scooter am richtigen Ort stehen, wenn die Nachfrage steigt.
- Ausreißer-Handling etablieren: Sehr lange Fahrten automatisch markieren (z. B. > Q3 + 1.5·IQR) und stichprobenartig prüfen (App/Backend, Abrechnung, Geofencing).
- KPI „Fahrten pro Ladung“ ableiten: Typische Fahrtdauer/-distanz als Input nutzen, um Kapazität und Ladezyklen abzuschätzen.
- Abbruchanalyse operationalisieren: Tageszeitklassen mit vielen Abbrüchen (absolut) als Priorität für Service-Interventionen behandeln; Klassen mit hoher Rate aber geringer Nachfrage eher als Hinweis für Ursachenanalyse.